Report - pg_randomness v1.1 released: PostgreSQL and Expected Random Byte Entropy for bytea
|
Obviously, the byte entropy of a purely random data string converges towards 8 bits. Uh, really? Let's have a look. Consider the following random string (which I observed malware was using): Listing 1: Byte entropy of a random string
$str_a = "Czi+wfIR9W/udXGwkUHw786u2zBXp1AFLMX49+ZRijSn40LF8f"; SELECT entropy($str_a); entropy --------- 5.01366 What is this? Although the string seems random, its entropy is far below 8. This is basically due to two reasons: a) The length of the string is short (50 bytes). Only for very large strings the byte entropy would converge towards 8 bits. This is simple to explain: If a string is shorter than 256 bytes, it doesn't have the possibility to consists of all 256 possible bytes, lowering the entropy. But even for strings greater or equal 256 bytes, a random string does not imply a uniform distribution of all bytes. A uniform distribution will only be approximated, if the string is sufficiently large. b) The alphabet size is < 256 bytes. As we can guess, the string is presumably base64 encoded. How do we know? We could e.g. count the number of distinct characters (use the PL/Python function bytea_nr_distinct_bytes, which is included in pg_randomness), which is in this case 35, and guess the alphabet size by rounding a little. Even for very large strings, the byte entropy will never reach 8 bits if not the entire alphabet size of 256 possible bytes is used in the string. In fact, the byte entropy of purely random base64/base32 data is bound to 6 bits/5 bits at maximum, respectively. Easy to calculate for the general case: maximum byte entropy of alphabet size as = log2(as). These observation woke my interest: Given a string of length l and alphabet size as, which byte entropy can we expect for purely random data? pg_randomness in version 1.1 includes an SQL function expected_random_entropy() that does exactly this calculation. Just to give you an expression how that would look like, check out the following graph: 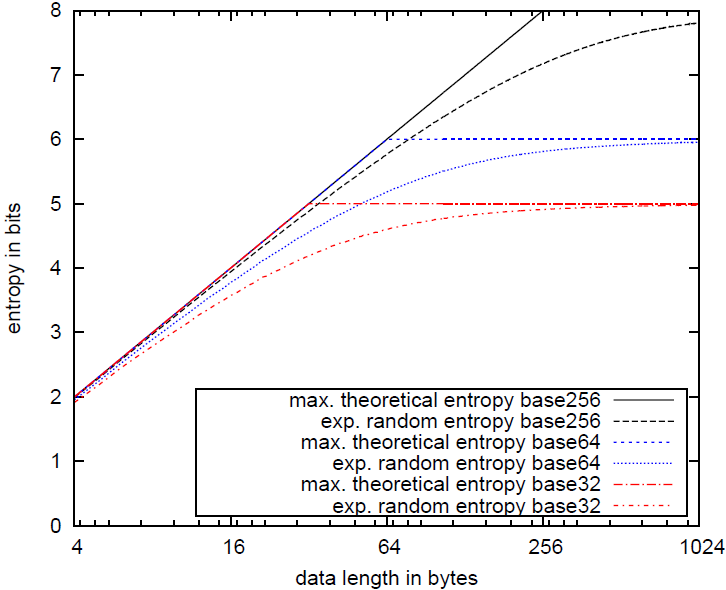
The graph shows the expected random entropies for the alphabet sizes 32, 64 and 256 and string lengths from 1 to 1024. Thanks to Chris for updating these graphs. As you can see, the expected entropies for random data significantly deviate from the maximum theoretical entropy given a uniform distribution. It also becomes obvious that taking into account the alphabet size is crucial to measure randomness. Coming back to our string $str_a, we calculate its expected entropy assuming it is base64 encoded: Listing 2: Expected random byte entropy example
SELECT expected_random_entropy($str_a); entropy --------- 5.00342 And instead of 8 bits, only an entropy of 5.00342 is expected, which is only 0.01 bits away from the actual string entropy. Although we cannot prove this, the string is very likely purely random. BTW, reversing the malware binary causing this string showed that it was RC4 encrypted, which leads to apparently random cipher texts. Bingo! :)
Yours
|

